Tento školský rok okrem rysovania kružníc a kruhov pridáme aj výpočet obvodu a obsahu kruhu či dĺžky kružnice a to aj v slovných úlohách. Po troche počítania sa vrátime k rysovaniu Tálesovej kružnice, dotyčníc ku kružnici ako aj vzájomným prienikom kružníc. Základom riešenia však určite zostane nakreslenie správneho náčrtu a zakreslenie aj farebných čiar a plôch v ňom. Preto nezabudnite pri riešení nasledujúcej kapitoly na rysovacie pomôcky, farbičky a kalkulačku.
Opakujeme z prvého stupňa
Môžete si pozrieť na obrazovke alebo vytlačiť a riešiť priamo v pracovných listoch.
Už dospeláckejšie.
Kružnica
Kružnica je množina bodov v rovine, ktoré majú od pevného bodu S (stredu kružnice) rovnakú vzdialenosť r (polomer kružnice).
Kruh
Kruh je množina bodov v rovine, ktorých vzdialenosť od pevného bodu S (stredu kružnice) je menšia alebo rovná polomeru danej vzdialenosti r (polomer kruhu). Obvod kruhu tvorí hraničná kružnica.
Polomer je vzdialenosť určená stredom kružnice (kruhu) a bodom na kružnici (obvode kruhu).
Priemer je vzdialenosť dvoch bodov na kružnici (obvode kruhu), pričom úsečka, ktorá ich spája prechádza stredom kružnice (kruhu).
Tetiva kružnice
Tetiva je úsečka, ktorej koncové body ležia na kružnici, ostatné body ležia vnútri kružnice. Najdlhšou tetivou je priemer kružnice. Os tetivy prechádza stredom kružnice.
1. Daná je kružnica k (S, 3 cm), Vyznač na nej tetivu AB, ktorá prechádzajú stredom S a tetivu CD, ktorá je kolmá na tetivu AB.
2. Daná je k (S, 4 cm) a bod N, ktorý leží vo vnútri k, pričom S ≠ N. Zostroj tetivu XY tak, aby N bol stred XY.
3. Je daná kružnica k(S; 5 cm). Narysuj tetivu, ktorá bude od stredu kružnice vzdialená 3 cm.
Vyvodenie Ludolfovho čísla alebo tzv. čísla pí (π)
Doplňte tabuľku. Odmerať môžete aj iné predmety. Vhodné je urobiť pokus na viacerých predmetoch. Lepšie je doplniť si aj ďalšie kruhy, ktoré vidíte okolo seba. Podiel odporúčame v treťom riadku vypočítať na kalkulačke na štyri desatinné čísla.
| dezertný tanier | plytký tanier | 2-eurovka | miska pod kvetináčom | |||
| obvod (mm) | ||||||
| priemer (mm) | ||||||
| podiel obvodu a priemeru |
Ak všetko pôjde dobre, aritmetickým priemerom hodnôt v treťom riadku získame číslo podobné číslu 3,1415. Výsledná hodnota závisí od presnosti merania a ďalších výpočtov. Pomer obvodu a priemeru toho istého kruhu nazývame Ludolfovým číslom alebo číslom pí.
Na matematike základnej školy budeme používať číslo pí v dvoch možnostiach vyjadrenia. Vždy necháme na vás, ktorá sa vám bude lepšie hodiť vo výpočte. π = 3,14 alebo π = 22/7.
Obvod kruhu, dĺžka kružnice
Obvod kruhu tvorí hraničná kružnica = dĺžka kružnice je o = 2πr alebo o = πd.

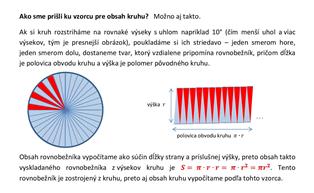
Prečo je to tak? Lebo podielom obvodu kruhu a jeho priemeru získame číslo pí, potom vyjadrením z tohto vzorca, dostaneme vzorec pre výpočet obvodu kruhu.
Obsah kruhu
Obsah kruhu je S = πr2 alebo S = π(d/2)2.
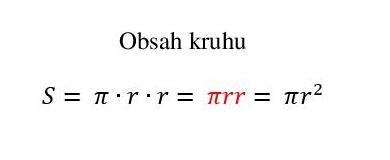
Prečo je to tak? Odporúčame pozrieť na týchto videách
https://www.youtube.com/watch?v=PBGQsQ_U8w0
https://www.youtube.com/watch?v=vl6cD80l73w
1. Vypočítajte dĺžku kružnice, ktorej polomer je 24 dm.
2. Vypočítajte dĺžku kružnice, ktorej polomer je 2 m.
3. Vypočítajte dĺžku kružnice, ktorej priemer je 100,4 m.
4. Aký polomer má kruh, ktorého obvod je 1000 m?
5. Vypočítajte obsah kruhu s polomerom 0,83 m.
6. Vypočítajte obsah kruhu, ktorého polomer je 37 cm.
7. Vypočítajte polomer kruhu, ktorého obsah je 2,0096 cm2.
8. Vypočítajte polomer kruhu, ktorého obsah je 113,04 dm2.
9. Vypočítajte obvod kruhu, ktorého obsah je 705,5 cm2.
10. Vypočítajte obsah kruhu, ktorého obvod je 59,66 cm.
Kružnicový oblúk
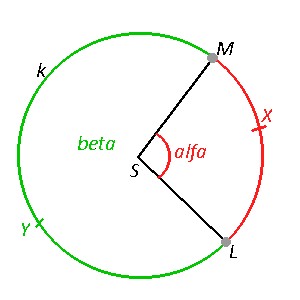
Kružnicový oblúk je časť kružnice ohraničená dvomi bodmi, ktoré ležia na kružnici. Body M a L rozdeľujú kružnicu na dva kružnicové oblúky:
Oblúk MXL = časť kružnice ohraničená krajnými bodmi M,L, ktorá obsahuje bod X
Alfa = stredový uhol prislúchajúci ku kružnicovému oblúku MXL
Oblúk MYL = časť kružnice ohraničená bodmi M,L, ktorá obsahuje bod Y
Beta = stredový uhol prislúchajúci ku kružnicovému oblúku MYL
Dĺžku kružnicového oblúka prislúcha k veľkosti uhlu v danej kružnici. Dĺžku kružnicového oblúka preto vypočítame ako podiel dĺžky celej kružnice a 360° vynásobený veľkosťou príslušného uhla v stupňoch. oalfa = o / 360° . alfa alebo oalfa = 2πr / 360° . alfa alebo oalfa = πd / 360° . alfa
Kruhový výsek
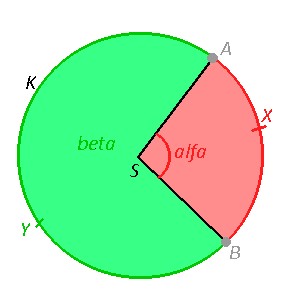
Kruhový výsek je časť kruhu, ktorú ohraničujú dva polomery SA, SB, ktoré rozdeľujú kruh na dva kruhové výseky.
Kruhový výsek ASB = obsahuje bod X
Kruhový výsek ASB = obsahuje bod Y
Obsah kruhového výseku prislúcha k veľkosti uhlu v danom kruhui. Obdah kruhového výseku preto vypočítame ako podiel obsahu celého kruhu a 360° vynásobený veľkosťou príslušného uhla v stupňoch. Salfa = S / 360° . alfa alebo Salfa = πr2 / 360° . alfa
Pred počítaním príkladov odporúčame si pozrieť video: https://www.youtube.com/watch?v=-NmQAQp_nQA&pbjreload=101
1. Aká je v milimetroch dĺžka oblúka kružnice k (S, 68 mm), ktorý prislúcha stredovému uhlu 78°?
2. Aká je v centimetroch dĺžka oblúka kružnice k (S, 46 cm), ktorý prislúcha stredovému uhlu 30°?
3. Aká je v metroch dĺžka oblúka kružnice k (S, 74 m), ktorý prislúcha stredovému uhlu 72°?
4. Vypočítajte obsah kruhového výseku kruhu K (O,36 cm), ktorý prislúcha stredovému uhlu 52°.
5. Vypočítajte obsah kruhového výseku kruhu K (O,189 m), ktorý prislúcha stredovému uhlu 110°.
6. Vypočítajte obsah kruhového výseku kruhu K (O,5,4 dm), ktorý prislúcha stredovému uhlu 30°.
Pracovné listy na vytlačenie
Odporúčané videá na riešené úlohy pánom učiteľom Jozefom Zvolenským. Jožko, od vysokej sme sa nevideli, tak aspoň takto. A nemusím ich robiť ja.
https://www.youtube.com/watch?v=3VKQr3CADPY
https://www.youtube.com/watch?v=e_hm5FEwNPo
https://www.youtube.com/watch?v=9fN2iWf0GlI
https://www.youtube.com/watch?v=XLDIJy9hLoM
https://www.youtube.com/watch?v=l-q-I4PV2Y4
https://www.youtube.com/watch?v=fA-2VI6rRv4
Tálesova kružnica
Je množina vrcholov - mimo krajných bodov priemeru kružnice - pravých uhlov všetkých pravouhlých trojuholníkov s preponou, ktorou je priemer kružnice.

Priemer kružnice na obrázku je označený AB. Potom podľa poučky - objavu p. Thálesa z Milétsu - vyznačené trojuholníky a aj všetky podobne vytvorené na kružnici sú pravouhlé.
1. Narysuj úsečku PQ s dĺžkou 75 mm. Zostroj jej stred a pomenuj ho S. Narysuj kružnicu t so stredom v bode S a polomerom SQ. Zvoľ na kružnici rôzne body A, B, C tak, aby ani jeden sa nestotožnil s bodmi P, Q. Zostroj trojuholníky PQA, PQB, PQC. Zmeraj uhly PAQ, PBQ, PCQ. Over čo vidíš na obrázku vyššie.
2. Narysuj úsečku AB dlhú 8 cm. Zostroj nad ňou Tálesovu kružnicu a v nej rovnoramenný trojuholník ABC. Vypočítaj jeho obsah.
Narysuj podľa postupu:
1. narysuj úsečku SY dlhú 73 mm
2. zostroj stred úsečky SY (konštrukčne) a pomenuj ho O
3. narysuj nad úsečkou SY Tálesovú kružnicu a pomenuj ju t
4. zostroj uhol SYX s veľkosťou 75°
5. priesečník polpriamky YX a kružnice t pomenuj P
6. narysuj úsečku PS
Ako nazývame trojuholník PSY podľa veľkosti vnútorných uhlov a ako podľa dĺžok strán?
Vzájomná poloha priamky a kružnice
1. Naryuj podľa postupu:
1. Naryuj kružnicu k so stredom v bode S a polomerom 6 cm. Na kružnici k zvoľ bod M.
2. Narysuj úsečku SM. Narysuj modrou farbičkou priamku p kolmú na úsečku SM, tak, aby prechádzala bodom M.
Modrá priamka p je dotyčnicou ku kružnici k.
2. Narysuj podľa postupu:
1. Narysuj úsečku SN dlhú 7 cm.
2. Narysuj kružnicu k so stredom v bode S a polomerom 4 cm.
3. Zostroj stred úsečky SN (konštrukčne) modrou farbičkou a pomenuj ho O. Narysuj kružnicu t so stredom v bode O a polomerom ON. Priesečníky kružnice t a kružnice k označ modrou farbou a pomenuj A a B.
4. Narysuj modrou farbičkou priamky NA a NB.
Modré priamky NA a NB nazývame dotyčnicami ku kružnici k, ktoré prechádzajú bodom N.
Vzájomná poloha dvoch kružníc
1. Na kružnici k1(S, r = 3,5 cm) zvoľte bod O. Zostrojte kružnice k2(O, r = 1,5 cm) a k3(O, r = 4 cm). Určte vzájomnú polohu kružníc k1 a k2; k1 a k3; k2 a k3.
2. Dané sú kružnice k1(S1,5 cm) a k2(S2,8 cm), pričom vzdialenosť ich stredov |S1S2| = 10 cm. Určte vzájomnú polohu.
3. Na číselnej osi okolo čísla 7 narysovali kružnicu s polomerom 6 a okolo čísla - 4 narysovali kružnicu s polomerom 5. Urči vzájomnú polohu kružníc.
4. Na číselnej osi okolo čísla - 10 narysovali kružnicu s polomerom 3,5 a okolo čísla - 6 narysovali kružnicu s polomerom 7,5. Urči vzájomnú polohu kružníc.
Množina bodov danej vlastnosti
Odporúčame pozrieť si videá (videá sú staršieho dáta)
https://www.youtube.com/watch?v=WvJQC67Ifdc
https://www.youtube.com/watch?v=2tUckOXX3TY
Vytlačte si pracovné listy. Prípadne dvojmo. Pracujte v nich najrv len kreslením a rozmýšľaním a až potom rysujte.
Odporúčeme aj videá p. učiteľa Jozefa Zvolenského
https://www.youtube.com/watch?v=YQc7EdA6Y8Q
https://www.youtube.com/watch?v=-7mfmoGBcEc
https://www.youtube.com/watch?v=fsdBsMt06Dc
Testy
https://www.skolske.sk/clanok/52946/8-rocnik--kruh-a-kruznica
https://www.skolske.sk/clanok/52944/ucime-sa-doma-talesova-veta