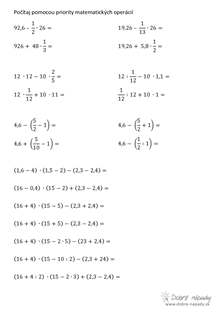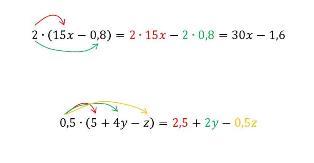Opakujeme číselné výrazy s ôsmakmi. Zápis súčtu, rozdielu, súčinu i podielu a ich kombinácie. Precvičujeme riešenie číselných výrazov s prijoritou matematických operácii. Zapisujeme slovne povedaný číselný výraz a naopak.
Začíname s výrazmi s premennou. Pripravujeme sa na riešenie lineárnych rovníc s jednou neznámou.
Číselný výraz je výraz zapísaný pomocou čísel, matematických operácii a zátvoriek.
sčítanec + sčítanec + ... + sčítanec = súčet23,24 + 15 + 8,6 + 78,15 = 8,24 + 2,67 + 65 = 19, 14 + 16,89 + 57 = |
menšenec - menšiteľ = rozdiel120 - 18,9 = 12,789 - 5 = 89,04 - 76,1 = |
činiteľ . činiteľ . ... . činiteľ = súčin34 . 2 . 0,5 = 1,1 . 0,4 . 11 = 0,75 . 3 . 4 . 10 = |
delenec : deliteľ = podiel34 : 17 = 1 280 : 40 = 11,7 : 0,5 = |
odporúčame video https://www.youtube.com/watch?v=UXRhG7nC6-g
Priorita matematických operácii
12 - 3,4 + 7 + 0,7 - 1 = podľa stupienka víťazov vidíme, že + a - sú na jednom mieste, preto nie je ani jedno dôležitejšie ako druhé, počítame zľava do prava =
15 . 2 : 3 : 10 . 9 = podľa stupienka víťazov vidíme, že . a : sú na jednom mieste, preto nie je ani jedno dôležitejšie ako druhé, počítame zľava do prava =
2 + 7 . 0,3 - 0,3 . 5 = podľa stupienka víťazov vidíme, že . je vyššie na stupni víťazov, preto počítame s ním skôr a ostatné odpíšeme v poradí, v akom sa nachádza. = 6 - 2,6 + 7 = 10,4
1,5 . 4 - 2 . 1,3 + 7 = 6 - 2,6 + 7 =
1 + (67 - 25) . 7 = podľa stupienka víťazov vidíme, že () je vyššie na stupni víťazov, preto ju počítame skôr a ostatné odpíšeme v poradí, v akom sa nachádza. = 1 + 42 . 7 = 1 + 294 = 295
8 . 9 + (87 - 9 . 9) = 72 + (87 - 81) =
Ďalšie pracovné listy nájdete tu https://www.dobre-napady.sk/pre-skolakov/hrame-sa-s-cislami/ciselne-vyrazy
Členy výrazu
Číselný výraz sa skladá z členov. Členy sú oddelené znamienkami + alebo - .
Jednočlenný výraz môže byť jedno číslo. Napríklad: 18 alebo - 7 alebo 6,2.
Jednočlenný výraz môže byť súčin alebo podiel dvoch a viacerých čísel. Napríklad: 1,8 . 6 alebo - 7 . (- 6) . 3 alebo 27 : 0,9.
Dvojčlenný výraz môže byť napríklad: 67 - 12 alebo 2 . 4 + 7 alebo 4 : 2 - 7 . 1 . 0,7 alebo 100 - 20 . 0,56.
Trojčlenný výraz môže byť napríklad: 67 - 12 - 6 alebo 2 . 4 + 7 - 8,9 alebo 4 : 2 - 7 : 10 . 0,7 - 8 alebo 100 - 20 . 0,56 + 1,5.
Podobne v štvorčlenných či viacčlenných výrazoch.
Zapisujeme číselný výraz podľa slovného zadania
1. O päť menšie ako štrnásť. Riešenie: 14 - 5
2. Päťkrát menšie ako 14. Riešenie: 14 : 5
3. O päť väčšie ako štrnásť. Riešenie: 14 + 5
4. Päťkrát väčšie ako štrnásť. Riešenie: 14 . 5
5. Rozdiel čísel 18 a 7 zväčšený o 2,14. Riešenie: (18 - 7) + 2,14
6. Rozdiel čísel 18 a 7 zmenšený o 2,14. Riešenie: (18 - 7) - 2,14
7. Rozdiel čísel 18 a 7 zväčšený dvakrát. Riešenie: (18 - 7) . 2
8. Rozdiel čísel 18 a 7 zmenšený dvakrát. Riešenie: (18 - 7) : 2
odporúčame video https://www.youtube.com/watch?v=52191s-jLXg
Pracovné listy na vytlačenie
Roznásobenie zátvorky, vynímanie pred zátvorku a porovnanie výrazov
Ako riešime úlohy s prienikom https://www.youtube.com/watch?v=44D-0W_j4zY&list=PLuiWINIVOv2xvn087WKUwGXvCTMm65ULt&index=6
Ako riešime úlohy "hadíkmi"
odporúčame video https://www.youtube.com/watch?v=pknpNJthwLQ
Ako riešime úlohy kreslením https://www.youtube.com/watch?v=MTD-Io0os2c
Výraz s premennou
Výraz s premennou je výraz zapísaný pomocou čísel, písmen (ktoré predstavujú akési zamaskované čísla), matematických operácii, znakov a zátvoriek.
odporúčame video https://www.youtube.com/watch?v=ewZ-N9Ec4io
Zapisujeme výraz s premennou podľa slovného zadania
1. O päť menšie ako číslo C. Riešenie: C - 5
2. Päťkrát menšie ako číslo C. Riešenie: C : 5
3. O päť väčšie ako C. Riešenie: C + 5
4. Päťkrát väčšie ako C. Riešenie: C . 5
5. Rozdiel čísel C a 7 zväčšený o 2,14. Riešenie: (C - 7) + 2,14
6. Rozdiel čísel C a 7 zmenšený o 2,14. Riešenie: (C - 7) - 2,14
7. Rozdiel čísel C a 7 zväčšený dvakrát. Riešenie: (C - 7) . 2
8. Rozdiel čísel C a 7 zmenšený dvakrát. Riešenie: (C - 7) : 2
9. Súčet čísel X a Y zväčšený dvakrát. Riešenie: (X + Y) . 2
10. Súčet čísel X a Y zmenšený dvakrát. Riešenie: (X + Y) : 2
11. V stanovom tábore bolo x stanov po 6 lôžok a y stanov po 4 lôžka. Koľko lôžok bolo v stanovom tábore? Riešenie: x . 6 + y . 4 = 6x + 4y
12. V jednom vagóne je 6 kupé po 8 sedadiel. Koľko najviac cestujúcich môžeme previesť vlakom, v ktorom je v takýchhto vagónov? Riešenie: v . 6 . 8 = 48v
Pracovné listy na vytlačenie
Členy výrazu
Výraz s premennou sa skladá z členov. Členy sú oddelené znamienka + alebo - .
Jednočlenný výraz môže byť jedno číslo. Napríklad: 2x alebo - c alebo y : 3
Dvojčlenný výraz môže byť napríklad: 67 - 12x alebo 2 . a + 7 alebo a : 2 - 7 . c alebo 100 - 20a
Trojčlenný výraz môže byť napríklad: 67 - 12x - 6y alebo 2 . a + 7 - b alebo x : 2 - 7 : 10y - 8z alebo 100 - 20 . a + 1,5b
Podobne v štvorčlenných či viacčlenných výrazoch.
Opačný výraz
Podobne ako pri celých číslach. K číslu 7 je opačné - 7. K číslu - 0,5 je opačné 0,5.
K výrazu 3x je opačný výraz - 3x. K výrazu - 0,3y je opačným výraz 0,3y.
K výrazu 2 - 4x je opačný - 2 + 4x.
K výrazu 3y + 2a je opačný - 3x - 2a.
Ak chceme získať opačný výraz, potom v pôvodnom výraze zmeníme znamienka na opačné.
Sčítavame a odčítavame výrazy s premennou
Vo výraze 5y = 5 . y číslo 5 voláme číselný koeficient
Koeficient pri jednočlene z je 1, lebo 1 . z = 1z = z
Koeficient pri jednočlene - z je - 1, lebo - 1 . y = - 1y = - y
Výrazy s tou istou premennou sčítame tak, že sčítame ich číselné koeficienty a premennú opíšeme. Napríklad: 2y + 3y = 5y
Výrazy s tou istou premennou odčítame tak, že odčítame ich číselné koeficienty a premennú opíšeme. Napríklad: 2y - 3y = - 1y = - y
- 4x + 2x = - 2x
3a - 7 + 12 - 10a = najprv si združíme jednotlivé členy k sebe podľa premennej (písmena) = 3a - 10a - 7 + 12 = - 7a + 5
0,4b - c + 1,3b - 2,5c =združenie nemusíme robiť, je to len pomôcka = 1,7b - 3,5c
- 8x + z + 6 - 3z + 2x - 6 = najprv si združíme jednotlivé členy k sebe podľa premennej (písmena) = - 8x + 2x + z - 3z + 6 - 6 = - 6x - 2x
8x + z + 6 - 3z + 2x = najprv si združíme jednotlivé členy k sebe podľa premennej (písmena) = - 8x + 2x + z - 3z + 6 = - 6x - 2x + 6
Sčítaním alebo odčítaním výrazov získame výraz s menším počtom členov, preto tiež môžeme hovoriť o tzv. zjednodušení výrazu. Aj každej inej úprave výrazu kedy zmenšíme počet členov hovoríme o zjednodušení výrazu.
Odporúčame videá
https://www.youtube.com/watch?v=frSevvftpaM
Zjednoduš výrazy
| 2a + 3a - a = | 2y + 0,5y - 0,5y = | - 2a + 3a - a = | 2s + s - 10s - 2 = |
| - 2a + 3 - a = | 2x + 0,5y - 0,5y = | - 2a + 3a - y = | 2s + 3 - 10s - 2 = |
| - 2a + 3 - a - 3,7= | - 2x + 0,5 - 0,5y - 3x = | - 2a - 3a + 2y = | 2d + 3d - 10s - 2s = |
| 2a - 3 - a - 3,7a = | 2x + 0,5 + 0,5y - 0,3x = | 0,2a - 3a - 2y = | -2d - 3d - s + 2s = |
Násobenie výrazov
odporúčame video https://www.youtube.com/watch?v=nWWsuUUJsjk&list=PLyB1n_kxEgEt45z7T_8mhyjVh1XXMYX8O&index=32&t=0s
2 . 3C =
2a . 5 =
2S . 6D =
5a . 2b =
7a . d =
b . 3a =
Roznásobujeme zátvorku
odporúčame video https://www.youtube.com/watch?v=gqSB1TfsLZs alebo https://www.youtube.com/watch?v=DHEaqSbdMvs
Roznásobte
| 2 . (2y + 3a) = | 5 . (2 . y + 3 . a) = | -0,2 . (x - 0,5) = | 12 . (2y + 3a) = |
| -2(0,2 + 3a) = | 20(0,2 + 30b) = | - 5(1 - 30b) = | 20(a - 30b - 10e) = |
| (a - b) . 5 = | (2x + 4) . 0,5 = | (7 - 5c) . (-1) = | (3x + 6y - 50) . 0,1 = |
| (- 1) . (- x + 0,2) = | - 1 . (- x - 2) = | - 1 . (- x - 2y) = | - (x + y - 2) = |
Vynímame pred zátvorku
Vyjmi pred zátvorku číslo 2
24x + 16 = 2 . (12x + 8) = 2(12x + 8) 24x + 16y - 6 = 2 . (12x + 8y - 3) = 2(12x + 8y - 3)
- 24x + 16a = 2(- 12x + 8a) = vymeníme poradie členov v zátvorke, nezvykne sa ako prvý písať záporný člen = 2(8a - 12x)
Vyjmi pred zátvorku číslo 4
24x + 16 = 4(6x + 4) 24x + 16y - 20 = 4(6x + 4y - 5)
- 24x + 16a - 8 = 4(- 6x + 4a - 2) = vymeníme poradie členov v zátvorke, nezvykne sa ako prvý písať záporný člen = 4(4a - 6x - 2)
Vyjmi pred zátvorku číslo - 1
24x - 16 = - 1 . (- 24x + 16) = - (- 24x + 16) = - (16 - 24x) 24x + 16y - 20 = - 1 . (- 24x - 16y + 20) = - (20 - 24x - 16y)
Vyjmi z výrazu 45a - 30c + 60 pred zátvorku číslo 15.
Vyjmi z výrazu 45a - 30c + 15 pred zátvorku číslo - 15.
Vyjmi z výrazu 4,5a - 3c - 6 pred zátvorku číslo 1,5.
Vyjmi z výrazu 4,5a - 3c + 1,5 pred zátvorku číslo - 1,5.
Vyjmi pred zátvorku čo najväčšie prirodzené číslo
24x - 16 = 8 . (3x - 2) = 8(3x - 2)
24x + 16y - 20 = 4 . (6x + 4y - 5)
36 - 18A - 30B =
- 25C - 30A + 15 =
Vynímať môžeme aj za zátvorku. Pozrite si spôsoby zápisu.
24x + 16y - 20 = - 1 . (- 24x - 16y + 20) = - (20 - 24x - 16y) alebo za zátvorku 24x + 16y - 20 = (- 24x - 16y + 20) . (- 1) = - (20 - 24x - 16y) . (- 1)
4,5a - 3c + 1,5 = 1,5 . (3a - 2c + 1) alebo za zátvorku 4,5a - 3c + 1,5 =
24x + 16y - 20 = 4 . (6x + 4y - 5) alebo za zátvorku 24x + 16y - 20 =
Pre zopakovanie odporúčame videá pán Zvolenského
https://www.youtube.com/watch?v=4UccgexyWyc
https://www.youtube.com/watch?v=5x3i6qCt3L8
Počítame hodnotu výrazu pre vstupné hodnoty
Vypočítaj hodnotu výrazu X + 45,15 pre X = 18. Riešenie: 18 + 45,15 = 63,15
Vypočítaj hodnotu výrazu X + 45,15 pre X = - 8. Riešenie: - 8 + 45,15 =
Vypočítaj hodnotu výrazu 5 . X + 45,15 pre X = 1,5. Riešenie: 5 . 1,5 + 45,15 =
Vypočítaj hodnotu výrazu 5 . X + 45,15 pre X = - 1. Riešenie: 5 . (- 1) + 45,15 =
Vypočítaj hodnotu výrazu 2y - 14 pre y = 1,5. Riešenie: 2 . 1,5 - 14 =
Vypočítaj hodnotu výrazu 2y - 14 pre y = - 2. Riešenie: 2 . (- 2) - 14 =
Vypočítaj hodnotu výrazu 15 - 2y pre y = 15. Riešenie: 15 - 2 . 15 =
Vypočítaj hodnotu výrazu 5 - 2y pre y = - 1,5. Riešenie: 15 - 2 . (- 1,5) =
Vypočítaj hodnotu výrazu 2(y - 14) pre y = 9. Riešenie: 2(9 - 14) =
Vypočítaj hodnotu výrazu 2y - 14(10 - y) pre y = 1,5. Riešenie: 2 . 1,5 - 14(10 - 1,5) =
odporúčame video https://www.youtube.com/watch?v=Ry4NBftWpSw
Pracovné listy na vytlačenie
Staršie pracovné listy (ešte z čias kedy sa výrazy a rovnice preberali v siedmej triede) na docvičenie nájdete tu https://www.dobre-napady.sk/pre-skolakov/hrame-sa-s-cislami/vyrazy
Problémová úloha - kódovanie v praxi