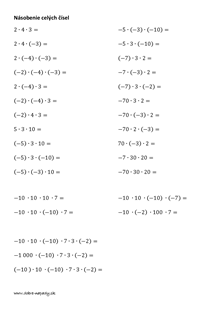O chvíľu začne nový školský rok. A ja s ním aj s mojimi ôsmakmi. Ako prvé učivo máme robiť na matematike celé čísla. Nuž som strávila pár dní prázdnin prípravou na tieto hodiny.
Dúfam, že to takto lepšie zvládneme. Čo si povieme v škole, to si môžu prečítať aj tu a pozrieť na videách. Tí, čo chýbajú sa už nebudú môcť vyhovárať, že si nevedeli nájsť učivo v edupage, že zabudli heslo... Už len, nech si nezabúdajú zošity, perá, farbičky a rysovacie pomôcky.
Čo sú to celé čísla
Celé čísla sa skladajú z prirodzených čísel (1, 2, 3, 4, …), nuly (0) a záporných čísel (−1, −2, −3, −4, …). Množina celých čísel sa v matematike väčšinou označuje Z, podľa Zahlen (nemecky čísla).
Z = {... - 7, - 6, - 5, - 4, - 3, - 2, - 1, 0, 1, 2, 3, 4, 5, 6, 7, ...}

nekladné čísla = celé záporné čísla + nula nezáporné čísla = celé kladné čísla + nula
Odporúčame videá
https://www.youtube.com/watch?v=Vi4RqSV6aNY
https://www.youtube.com/watch?v=H8asW94YxhI
Celé čísla používame aj pri zaznamenávaní peňazí. Dlhy značíme zápornými číslami. Nazývame ich aj červenými. Prečo? V minulosti sa dlžobné úpisy podpisovali krvou a z tej doby zostali červené čísla. Teda ak niekto povie, že jeho firma je v červených číslach, zamená to, že sa mu nedarí a ide do krachu. Naopak. Ak niekto povie, že jeho firma sa už dostala z červených čísel do čiernych, už je na tom lepšie a zbavil sa dlhov. Čierne čísla sú zase prirovnaním k čiernemu atramentu, ktorý sa kedysi používal na písanie.
V niektorých krajinách a aj v našich alternatívnych učebniciach sa zvykne učiť počítanie s celými číslami práve podľa farby. Červené sú dlhy a čierne sú zárobky. Napríklad: 2 + 3 = 5 alebo 2 + 3 = 1 alebo 2 + 3 = 5 alebo 2 + 3 = 1
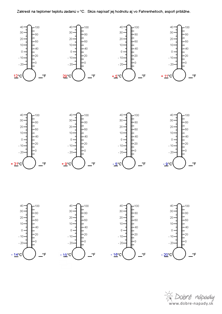
Zobrazenie čísel na osi, absolútna hodnota čísla, porovnanie celých čísel

Vzdialenosť ľubovoľného čísla na číselnej osi od nuly je počet dielov, ktoré sú medzi daným číslom a nulou. Napríklad číslo - 12 sa od nuly nachádza 12 dielov. Alebo číslo - 3 sa nachádza 3 diely od nuly. Číslo 14 je od nuly vzdialené 14 dielov. Túto vzdialenosť nazývame absolútna hodnota čísla.
Absolútnou hodnotou čísla nazývame vzdialenosť čísla od nuly. Absolútnu hodnotu zapisujeme pomocou zápisu, ktorý pripomína dĺžku úsečky alebo vzdialenosť dvoch bodov z geometrie.
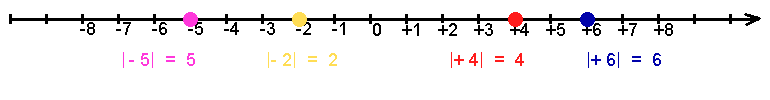
Navzájom opačné čísla sú čísla stredovo súmerné podľa čísla 0. Napríklad číslo - 4 je opačné k číslu 4 alebo číslo 7 je opačné k číslu - 7. Súčet opačných čísel je 0.
Porovnávanie celých čísel
Ľubovoľné kladné číslo je väčšie ako záporné.
Z dvoch kladných čísel je väčšie to, ktoré je na číselnej osi ďalej od nuly.
Z dvoch záporných čísel je väčšie to, ktoré je bližšie k nule.
Porovnávanie čísel je vhodné robiť zo začiatku zakresľovaním na číselnej osi. Môžeme si urobiť pomôcku. Na dlhý úzky pás papiera si narysujeme os, ktorý zložíme a môžeme nosiť v zošite.
Odporúčame video
https://www.youtube.com/watch?v=H8asW94YxhI
Pár úloh na precvičenie
1) Vypočítaj absolútnu hodnotu čísel 27 a -15.
2) Ktoré číslo má rovnakú absolútnu hodnotu ako číslo 67?
3) Urči číslo, ktoré sa nachádza v strede medzi číslami 19 a -19. pomôž si zakreslením na číselnej osi
4) Doplň vetu: "Absolútna hodnota ľubovoľného celého čísla je vždy _______________ číslo. "
5) Vypíš všetky celé čísla, ktorých absolútna hodnota je menšia ako 9. pomôž si zakreslením na číselnej osi
6) Vypíš všetky celé čísla, ktorých absolútna hodnota je väčšia ako 11 a zároveň menšia ako 15. pomôž si zakreslením na číselnej osi
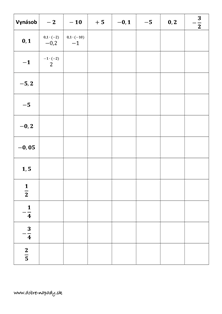
Násobíme a delíme celé čísla
Množina celých čísel Z je uzavretá pre operáciu násobenia (výsledkom násobenia ľubovoľných dvoch celých čísel je tiež celé číslo). Nie je však uzavretá pre operáciu delenia (výsledkom delenia ľubovoľných dvoch celých čísel nie je vždy celé číslo).
Vlastnosti súčinu a podielu dvoch celých čísel
Súčin dvoch celých čísel je komutatívna operácia, teda, ak a a b sú celé čísla, tak platí: a . b = b . a. Táto veta nám hovorí, že pri násobením dvoch celých čísel nezáleží na poradí činiteľov.
Súčin celých čísel je asociatívna operácia: ak a, b a c sú ľubovoľné celé čísla, tak platí: (a . b) . c = a . (b . c). Teda, pri súčine celých čísel možno činitele ľubovoľne združovať.
Ak a a b sú celé čísla a jedno z nich je záporné, tak výsledok násobenia alebo delenia je záporný. Napríklad: 5 . (- 1) = - 5 alebo - 6 . 2 = - 12 Ak je každé číslo z inej strany od nuly, potom je výsledok záporný.
Ak a a b sú celé čísla a obe sú záporné alebo obe sú kladné, tak výsledok násobenia a lebo delenia je kladný. Napríklad: - 5 . (- 1) = 5 alebo - 6 . (- 2) = 12 Ak sú obe čísla z jednej strany od nuly, potom je výsledok kladný.
Ak a je celé číslo, tak výsledok násobenia čísla a . 0 = 0 . a = 0. Napríklad: 5 . 0 = 0
Ak a je celé číslo, tak výsledok delenia čísla 0 : a = 0 naopak to však neplatí a : 0 = sa nedá. Nulou nedelíme! Prečo? Už si skúsil rozdeliť tortu na nula častí? Podarilo sa?
Pár úloh na precvičenie
1) Vypočítaj absolútnu hodnotu súčinu čísel 27 a - 9.
2) Vypočítaj súčin absolútnych hodnôt čísel 27 a - 9.
3) Vypočítaj absolútnu hodnotu súčinu čísel - 3 a -15.
4) Vypočítaj súčin absolútnych hodnôt čísel - 3 a -15.
5) Vypočítaj absolútnu hodnotu podielu čísel - 15 a - 3.
6) Vypočítaj podiel absolútnych hodnôt čísel -15 a - 3.
7) Vypočítaj absolútnu hodnotu podielu čísel 27 a - 9.
8) Vypočítaj podiel absolútnych hodnôt čísel 27 a - 9.
9) Absolútnu hodnotu čísla -7 vynásob číslom 6.
10) Absolútnu hodnotu čísla -7 vynásob absolútnou hodnotou čísla 6.
11) Absolútnu hodnotu čísla -7 vynásob číslom - 8.
12) Absolútnu hodnotu čísla -7 vynásob absolútnou hodnotou čísla - 8.
13) Číslo -7 vynásob číslom 6.
14) Číslo -7 vynásob absolútnou hodnotou čísla - 6.
Občas skrátime násobenie číslom - 1 takto:
(- 1) . (- 2) = - (- 2) potom pre zjednodušenie vieme tento zápis napísať bez zátvorky + 2, lebo platí pravidlo o znamienkach pri násobení popísané vyššie.
(- 1) . (+ 2) = - (+ 2) potom pre zjednodušenie vieme tento zápis napísať bez zátvorky - 2, lebo platí pravidlo o znamienkach pri násobení popísané vyššie.
15) Zapíš čísla -(-2); -(-7); -(+9); -(+14); +(-7); +(-11); +(+67); +(+8) v zjednodušenom tvare bez zátvoriek.
Sčítavame a odčítavame celé čísla
Množina celých čísel Z je uzavretá pre operácie sčítania (výsledkom sčítania ľubovolných dvoch celých čísel je tiež celé číslo) a odčítania (výsledkom odčítania ľubovolných dvoch celých čísel je tiež celé číslo).
Odporúčame videá
https://www.youtube.com/watch?v=LtkGHZzpkeo
https://www.youtube.com/watch?v=5lJe2EYvdqw
Vlastnosti súčtu dvoch celých čísel
Súčet dvoch celých čísel je komutatívna operácia, teda, ak a a b sú celé čísla, tak platí: a + b = b + a. Táto veta nám hovorí, že pri sčítaní dvoch celých čísel nezáleží na poradí sčítancov. Napríklad: 5 + (-1) = (-1) + 5 = 4
Súčet celých čísel je asociatívna operácia: ak a, b a c sú ľubovoľné celé čísla, tak platí: (a + b) + c = a + (b + c). Teda, pri sčítaní celých čísel možno sčítance ľubovoľne združovať.
Celé číslo 0 je neutrálnym prvkom operácie „sčítanie celých čísel“, teda, ak je a ľubovoľné celé číslo, tak a + 0 = 0 + a = a. Táto veta vraví, že ak pri sčítaní celých čísel je jedným zo sčítancov 0, tak súčet sa rovná druhému sčítancu. Napríklad: 0 + (-1) = (-1) + 0 = -1
Ku každému celému číslu a existuje tzv. opačné celé číslo (-a), pre ktoré platí: a + (-a) = (-a) + a = 0. Vzájomne opačné čísla majú tú vlastnosť, že keď ich sčítame, dostaneme súčet, ktorý je rovný číslu 0. Napríklad: opačné číslo k číslu 4 je číslo - 4.
Pár úloh na precvičenie
1) Vypočítaj absolútnu hodnotu súčtu čísel 27 a -15.
2) Vypočítaj súčet absolútnych hodnôt čísel 27 a -15.
3) Vypočítaj absolútnu hodnotu súčtu čísel -7 a -15.
4) Vypočítaj súčet absolútnych hodnôt čísel -7 a -15.
5) Vypočítaj absolútnu hodnotu rozdielu čísel -7 a -15.
6) Vypočítaj rozdiel absolútnych hodnôt čísel -7 a -15.
7) Vypočítaj absolútnu hodnotu rozdielu čísel 27 a -15.
8) Vypočítaj rozdiel absolútnych hodnôt čísel 27 a -15.
9) Asi jeden z najznámejších matematikov (pamätajú si ho aj herci) je Pytagoras. Narodil sa v roku 580 pred Kristom a zomrel v roku 496 pre Kristom.
a) Koľko rokov sa dožil Pytagoras?
b) Koľké výročie jeho narodenia sme oslávili tento rok?
10) Vo ôsmej triede v rámci geometrie sa viac učíme aj o Tálesovi, ktorého zaradili medzi šiestich mudrcov staroveku. Preslávil sa tzv. Talesovou vetou a riešením konštrukčných úloh o rovnoramenných trojuholníkoch v architektúre na čo neskôr nadviazali Pytagorejci. Narodil sa v roku 624 pred Kristom a zomrel v roku 546 pred Kristom.
a) Koľko rokov sa dožil Táles?
b) Koľké výročie jeho narodenia sme oslávili tento rok?
Iné pravidlá pre celé čísla
Ak a, b a c sú ľubovoľné celé čísla, tak platí: (a + b) . c = c . (a + b). Tzv. distributívnym zákonom môžeme roznásobiť zátvorku: (a + b) . c = a . c + b . c alebo c . (a + b) = c . a + c . b.
Napríklad
5 . (3 + 4) = 5 . 3 + 5 . 4 5 . (3 - 4) = 5 . 3 - 5 . 4
5 . (-3 + 4) = 5 . (-3) + 5 . 4 5 . (-3 - 4) = 5 . (-3) - 5 . 4
V číselnom výraze aj s celými číslami platí naďalej, že najrv riešime zátvorky, potom násobíme a delíme, až potom sčítame a odčítame.
Kladné a záporné desatinné čísla a zlomky...
Pridáme si k celým číslam aj desatinné čísla a zlomky, ktoré tiež môžu byť kladné aj záporné. Vytlačte si a riešte pracovné listy. Aplikujte všetko, čo sme robili v predošlých úlohách na celých kladných a záporných číslach.
Pár úloh na precvičenie
1) Vypočítaj absolútnu hodnotu čísel 2,7 a - 0,15.
2) Ktoré číslo má rovnakú absolútnu hodnotu ako číslo 6,07?
3) Vypočítaj absolútnu hodnotu súčtu čísel 2,7 a - 0,15.
4) Vypočítaj súčet absolútnych hodnôt čísel 2,7 a - 0,15.
5) Vypočítaj absolútnu hodnotu súčtu čísel - 7 a - 1,5.
6) Vypočítaj súčet absolútnych hodnôt čísel - 7 a - 1,5.
7) Vypočítaj absolútnu hodnotu podielu čísel - 1,5 a - 3.
8) Vypočítaj podiel absolútnych hodnôt čísel - 15 a - 0,3.
9) Vypočítaj absolútnu hodnotu podielu čísel 2,7 a - 9.
10) Vypočítaj podiel absolútnych hodnôt čísel 27 a - 0,9.
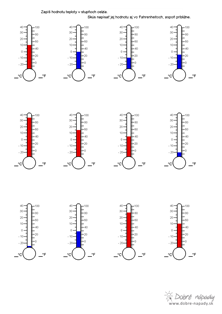
11) Zakresli na číselnú os čísla 1,5; 2,3; 4 modrou farbou a k nim opačné červenou farbou.
12) Nájdi medzi číslami 1,2; - 3; 6; 0,05; - 1; 3; -6; - 0,5; - 12 navzájom opačné čísla a zakrúžkuj ich rovnakou farbou.
13) Zapíš čísla -(-2); -(-0,7); -(+9); -(+1,4); +(-7); +(-1,1); +(+67); +(+0,8) v zjednodušenom tvare bez zátvoriek.
Pár pracovných listov na docvičenie nájdete aj na našom webe https://www.dobre-napady.sk/pre-skolakov/hrame-sa-s-cislami/category/114-cele-cisla
Ako ste zvládli učivo si môžete otestovať v testoch pre ôsmakov na našom webe
Pár videí s riešenými príkladmi
https://www.youtube.com/watch?v=5IvZ7XzxEMw
https://www.youtube.com/watch?v=PsQ-W85RXW8
https://www.youtube.com/watch?v=AL7F1RpJk9Q
https://www.youtube.com/watch?v=0hFQJQp6qa4