V siedmom ročníku sa učíme povrch a objem kocky a kvádra, prípadne pravidelného štvorbokého hranola. Najprv si kocky a kvádre narysujeme vo voľnom rovnobežnom premietaní. Naučíme sa rozlíšiť nadhľad a podhľad ľavotočivý aj pravotočivý. Pripomenieme si premenu jednotiek dĺžky a obsahu, vysvetlíme si premenu jednotiek objemu v metrickej miere a jej prepojenie na dutú mieru. Prejdeme výpočtami podľa vzorcov, celé učivo ukončíme zaujímavými slovnými úlohami.
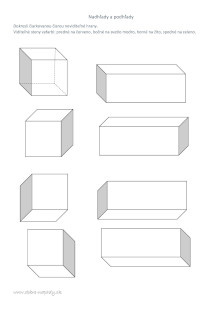
Pre zopakovanie stavieb z kociek
https://www.dobre-napady.sk/pre-skolakov/tipy-pre-skolakov/1582-stavby-z-kociek
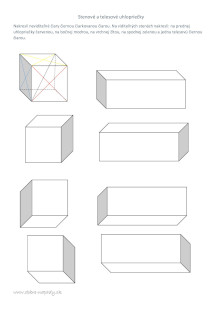
Ľavotočivý a pravotočivý nadhľad
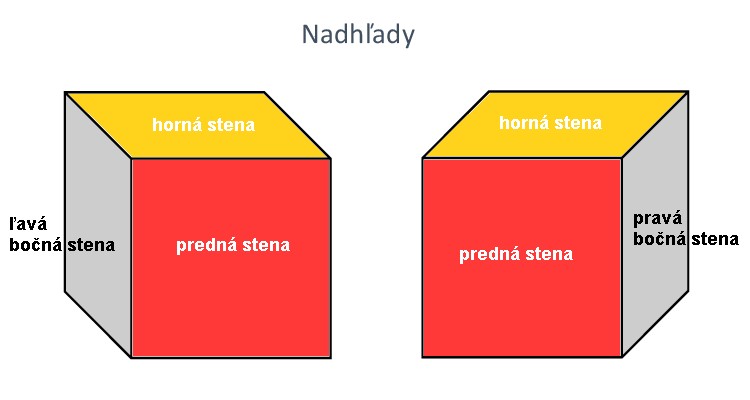
Pri nadhľade vidíme na kocke okrem prednej steny vždy aj vrchnú stenu a podľa toho, či vidíme ľavú alebo pravú bočnú stenu, hovoríme o ľavotočivom nadhľade alebo pravotočivom nadhľade. Pri rysovaní takýchto modelov hrany, ktoré vidíme priamo - dĺžka a výška si zachovávajú svoj rozmer, ale hrana, ktorú nevidíme priamo - šírka alebo hĺbka sa rysuje pod uhlom 135° a jej veľkosť je zmenšená na polovicu. Tieto úpravy robíme pretože náš zrak takto vníma telesá zobrazené v rovine.
Odporúčame videá: https://www.youtube.com/watch?v=IuZBxT4OVPg a https://www.youtube.com/watch?v=TenexDwizEU
1. Narysuj pravotočivý model kocky s dĺžkou hrany 5 cm.
2. Narysuj pravotočivý model kvádra s dĺžkou 8 cm, šírkou 5 cm a výškou 4 cm.
3. Narysuj ľavotočivý model kvádra s dĺžkou 6 cm, šírkou 5 cm a výškou 4 cm.
Ľavotočivý a pravotočivý podhľad
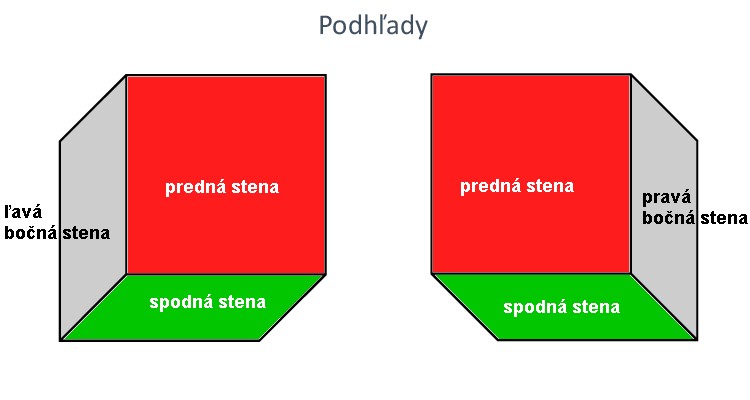
Pri podhľade vidíme na kocke okrem prednej steny vždy aj spodnú stenu a podľa toho, či vidíme ľavú alebo pravú bočnú stenu, hovoríme o ľavotočivom podhľade alebo pravotočivom podhľade. Pri rysovaní takýchto modelov hrany, ktoré vidíme priamo - dĺžka a výška si zachovávajú svoj rozmer, ale hrana, ktorú nevidíme priamo - šírka alebo hĺbka sa rysuje pod uhlom 135° a jej veľkosť je zmenšená na polovicu. Tieto úpravy robíme pretože náš zrak takto vníma telesá zobrazené v rovine.
Premena jednotiek
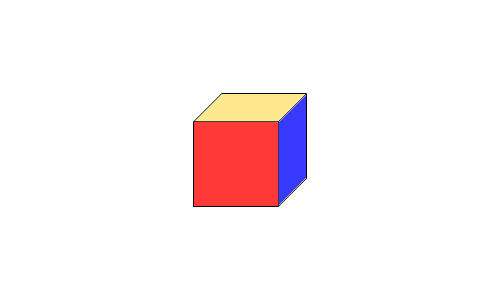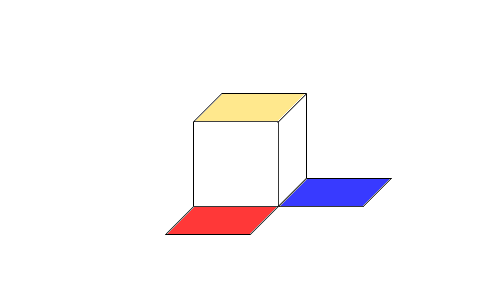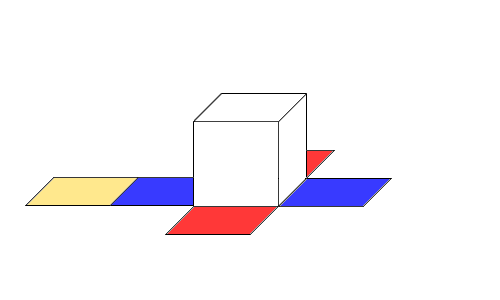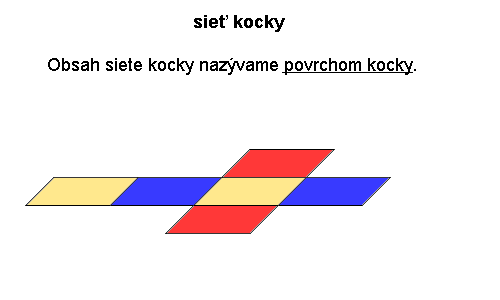
Povrch kocky a kvádra
Povrch značíme veľkým tlačeným písmenom S. Povrch je súčet obsahov stien telesa.
Kocka má 6 zhodných stien a každá stena má tvar štvorca.
Ak má kocka dĺžku hrany 5 cm, potom obsah jednej steny je 5 cm . 5 cm = 25 cm2. Všetky steny sú zhodné, preto aj ďalších päť stien má obsah 25 cm2. Potom povrch kocky bude 6 . 25 cm2 = 150 cm2.
Ak má kocka dĺžku hrany 4 cm, potom obsah jednej steny je 4 cm . 4 cm = 16 cm2. Všetky steny sú zhodné, preto aj ďalších päť stien má obsah 16 cm2. Potom povrch kocky bude 6 . 16 cm2 = 96 cm2.
Ak má kocka hranu dĺžky a, potom vzorec pre výpočet povrchu kocky je S = 6 . a . a
1) Vypočítaj povrch kocky s dĺžkou hrany 18 dm.
2) Vypočítaj povrch kocky s dĺžkou hrany 2,5 m.
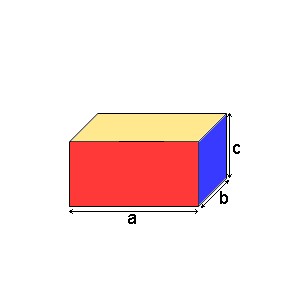
Kváder má 6 stien, pričom dve a dve oproti sebe sú zhodné.
Ak má kváder dĺžku 5 cm, šírku 3 cm a výšku 4 cm, potom obsah prednej steny je 5 cm . 4 cm = 20 cm2, obsah spodnej steny je 5 cm . 3 cm = 15 cm2 a obsah bočnej steny je 3 cm . 4 cm = 12 cm2. Uvedomíme si, že predná stena je rovnaká ako zadná, bočné steny sú dve a spodná a vrchná stena sú tiež zhodné. Preto povrch vypočítame 2 . (20 cm2 + 15 cm2 + 12 cm2) = 47 cm2.
Ak má kváder dĺžku 6 cm, šírku 3 cm a výšku 5,5 cm, potom obsah prednej steny je 6 cm . 5,5 cm = 33 cm2, obsah spodnej steny je 6 cm . 3 cm = 18 cm2 a obsah bočnej steny je 3 cm . 5,5 cm = 16,5 cm2. Uvedomíme si, že predná stena je rovnaká ako zadná, bočné steny sú dve a spodná a vrchná stena sú tiež zhodné. Preto povrch vypočítame 2 . (33 cm2 + 18 cm2 + 16,5 cm2) = 67,5 cm2.
Ak má kváder dĺžku a, šírku b a výšku c, potom vzorec pre výpočet povrchu kocky je S = 2 . (a . b + a . c + b . c) alebo S = 2 . a . b + 2 . a . c + 2 . b . c
1) Vypočítaj povrch kvádra s rozmermi 4 m, 22 dm, 18 dm.
2) Vypočítaj povrch kvádra s rozmermi 4,5 dm, 2 dm a 1,8 dm.
3) Zapíš vzorec pre povrch kvádra, ak dĺžku označíme x, šírku y a výšku v.
Objem kocky a kvádra
Objem značíme veľkým tlačeným písmenom V. Objem je množstvo tekutiny (môžem byť aj zemina, piesok, betón...), ktorá sa zmestí do vnútra telesa.
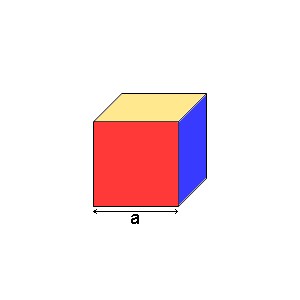

Kocka má 6 zhodných stien a každá stena má tvar štvorca. Spodná stena je štvorec a výška má rovnakú dĺžku ako hrana v podstave.
Ak má kocka dĺžku hrany 5 cm, potom obsah spodnej steny je 5 cm . 5 cm = 25 cm2. Výška kocky je tiež 5 cm. Ak budeme liať vodu do vnútra kocky, voda najprv pokryje dno (spodnú stenu) kocky = 25 cm2 a postupne ako lejeme, sa hladina zdvíha do výšky. Môžeme povedať, že celý štvorec - dno sa zdvíha hore. Preto objem kocky vypočítame 25 cm2 . 5 cm = 125 cm3.
Ak má kocka hranu dĺžky a, potom vzorec pre výpočet objemu kocky je V = a . a . a
1) Vypočítaj objem kocky, ktorej hrana má dĺžku 6,5 cm.
2) Vypočítaj objem kocky, ktorej hrana má dĺžku 7 dm.

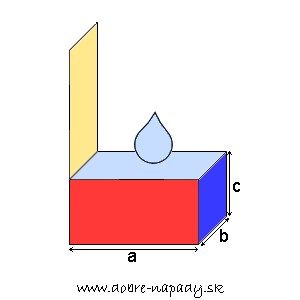
Kváder má 6 stien, pričom dve a dve oproti sebe sú zhodné.
Ak má kváder dĺžku 5 cm, šírku 3 cm a výšku 4 cm, potom obsah spodnej steny (dna) je 5 cm . 3 cm = 15 cm2. Výška kvádra je 4 cm. Ak budeme liať vodu do vnútra kvádra, voda najprv pokryje dno (spodnú stenu) kvádra = 15 cm2 a postupne ako lejeme, sa hladina zdvíha do výšky. Môžeme povedať, že celý obdĺžnik - dno sa zdvíha hore. Preto objem kvádra vypočítame 25 cm2 . 4 cm = 100 cm3.
Ak má kváder dĺžku a, šírku b a výšku c, potom vzorec pre výpočet objemu kocky je V = a . b . c
1) Vypočítaj povrch kvádra s rozmermi 4 m, 22 dm, 18 dm.
2) Vypočítaj povrch kvádra s rozmermi 4,5 dm, 2 dm a 1,8 dm.
3) Zapíš vzorec pre objem kvádra, ak dĺžku označíme x, šírku y a výšku v.
Úlohy na precvičenie
1) 1m3 skla váži 2 500 kg. Vypočítajte hmotnosť sklenej dosky s rozmermi 3 m a 4 m, ak hrúbka skla je 1 cm.
2) Koľko hektolitrov vody je napustených vo vonkajšom bazéne, ktorý je dlhý 4 m, široký 1,8 m a hlboký 1,2 m, ak voda siaha do výšky 40 cm?
3) Vypočítaj objem a povrch kocky, ktorá je zostavená z 27 malých kociek s dĺžkou hrán 3 cm.
4) Koľko minimálne tehál je potrebných na postavenie steny, ktorá má byť 60 m dlhá, 3 m vysoká a 30 cm široká, ak na 1 m3 potrebujeme 275 tehál?
5) Koľko m2 kože je potrebných na zhotovenie kufra tvaru kvádra s rozmermi 1 m a 0,8 m a 0,5 m, ak na záhyby a odpad musíme ešte pripočítať 15 % materiálu potrebného na vlastný povrch kufra?
6) Bazén má tvar kvádra s rozmermi dna 6 m a 25 m a výškou 2,5 m. Do akej výšky siaha voda v tomto bazéne, ak sme tam naliali 30 hl vody?
7) Debnička na kvety má tvar kvádra. Jej dĺžka je 1,3 m, šírka 15 cm a výška 1 m. Bude stačiť plné dvanásťlitrové vedro zeminy na jej naplnenia až po okraj?
8) O koľko centimetrov kubických sa zväčší objem kocky (centimetrov štvorcových sa zväčší povrch), ak zväčšíme hranu kocky o 4 cm?
9) Za aký čas naplní čerpadlo s výkonom 3 hl/minútu nádrž 3 m dlhú a 1,6 m širokú do výšky 75 cm?
10) Povrch kocky je 54 dm2. Vypočítaj jej objem v metroch kubických.
11) Do akvária s rozmermi dna 40 cm a 50 cm sme naliali 6 litrov vody. O koľko centimetrov stúpla hladina vody v akváriu?
12) Do bazéna v tvare kvádra s rozmermi dna 25 m a 12 m a výškou 3 m sme naliali vodu 5 cm pod okraj. Koľko hektolitrov vody je v bazéne?
Odporúčame videá pána učiteľa Jozefa Zvolenského:
https://www.youtube.com/watch?v=lMzitgU_11o
https://www.youtube.com/watch?v=3Ws6iGWiuYY